Унарная (единичная) система счисления
Унарная система счисления (единичная система счисления) — положительная суммарная целочисленная система счисления с основанием 1.
В качестве единственной «цифры» используется «1», чёрточка (|), камешек, костяшка счёт, узелок, зарубка и др.
Попытки записи чисел с целой и дробной частью только одной цифрой пока безуспешны.
Единичные системы счисления с весовыми функциями (коэффициентами) f=b независящими от положения цифр являются непозиционными (непоместными). Числа в них могут быть записаны в виде:
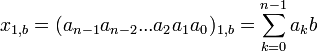, где:
n - число цифр (единиц),
k - число, порядковый номер цифры (единицы) в числе x1,b,
a - число, определяющее множество из которого берутся ak,
ak - числа из одноэлементного множества a={1} (единицы),
b - число, основание весовой функции,
при b=1 веса всех цифр одинаковые и равны «1»,
Так как весовой коэффициент - b может быть любым, то число единичных непозиционных систем счисления бесконечно. Наибольшее распространение получила единичная непозиционная система счисления с весовым коэффициентом равным единице (b=1). В народе иногда применяется единичная непозиционная система счисления с весовым коэффициентом равным двум (b=2), при счёте па?рами.
Из комбинаторики известно, что число записываемых кодов не зависит от основания весового коэффициента - b, который определяет диапазон представляемых числами x1,b величин, и равно числу размещений с повторениями:
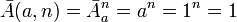, где:
a=1 - одноэлементное множество a={1} из которого берутся цифры ak, n - число элементов (цифр) в числе x1,b. Из этого следует, что вышеприведённая запись для фиксированного числа разрядов - n определяет одно число.
Сумма таких записей с числом разрядов n от 1 до n определяет n единичных чисел.
Целые числа записываются в виде:
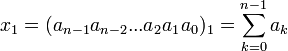, где:
ak - единицы.
Особенностью такой системы является то, что если приписать к числу одну «цифру» (единицу), то число увеличивается лишь на эту единицу.
(Для сравнения: если в обычной десятичной системе счисления к натуральному числу приписать справа 1, число увеличивается сразу в 10 раз — и плюс 1).
Поэтому такая система записи чисел обычно применяется там, где идёт последовательное увеличение подсчитываемой величины, например: при счёте числа дней, количества одинаковых событий и т. п.
Вероятно, подобная система является древнейшей системой счисления в истории человечества, для примера можно привести Московский математический папирус, датируемый приблизительно 1850 до н. э.
Дробные числа записываются в виде дроби из двух целых чисел:
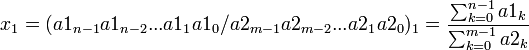, где:
n - число цифр числителя (a1) дробного числа x1,
m - число цифр знаменателя (a2) дробного числа x1.
Применение
- в первом классе начальной школы
- при подсчёте голосов на выборах в малых группах людей
- в коллективных хозяйствах (для учёта трудодней)
- в телефонных центрах (для подсчёта количества отработанных вызовов)
- в тюрьмах и при отбывании воинской повинности (для подсчёта числа дней)
- >Робинзоном Крузо для ведения календаря на необитаемом острове
- в домино при подсчёте очков
- Единичное кодирование
- Коды Голомба
- Машина Тьюринга
- в цифровой электронике одной унарной единице соответствует один инвертор с логикой на входе
- в дешифраторах
- в счётах, внутри одного разряда
- при фальсификации диагонального метода Кантора
- в вавилонской системе счисления применялось единичное кодирование десятичных цифр внутри шестидесятиричных разрядов
Подобно двоично-десятичному кодированию, в обычной десятичной системе счисления внутри каждого разряда возможно единичнодесятичное (унарнодесятичное) кодирование, в котором каждой арабской цифре от "0" до "9" соответствует свой единичный (унарный) код от "" до "111111111".
В обычной двоичной системе счисления, применяемой в вычислительной технике, внутри каждого разряда возможно использование единичнодвоичного (унарнодвоичного) кодирования, в котором каждой арабской цифре от "0" до "1" соответствует свой единичный (унарный) код от "" до "1".
В обычной троичной системе счисления, применяемой в вычислительной технике, внутри каждого разряда возможно применение единичнотроичного (унарнотроичного) кодирования, в котором каждой арабской цифре от "0" до "2" соответствует свой единичный (унарный) код от "" до "11".
В обычной четверичной системе счисления, применяемой в вычислительной технике, внутри каждого разряда возможно применение единичночетверичного (унарночетверичного) кодирования, в которой каждой арабской цифре от "0" до "3" соответствует свой единичный (унарный) код от "" до "111".
Если весовые коэффициенты b зависят от положения цифр (единиц) (b(k)=f(k)), то единичная система счисления является поместной (позиционной). Целое число в ней может быть записано в виде:
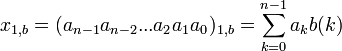, где:
b(k)=f(k) - числа весовой функции, весовые коэффициенты, зависящие от места (номера) цифры (единицы) в числе x1,b.
Пример: при bk=(k+1)
число 11 = 1*1 = 110,
число 111 = 1*2 + 1*1 = 310,
число 1111 = 1*3 + 1*2 + 1*1 = 610,
число 11111 = 1*4 + 1*3 + 1*2 + 1*1 = 1010.
При b(k)=f(k)=1 единичная система счисления может рассматриваться и как вырожденная поместная (позиционная) положительная целочисленная система счисления с основанием равным 1.
При межразрядной функции f(k)=b(k)=bk образуются сдвоенные единичные показательные системы счисления:
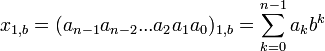, в которых множество a{1}, из которого берутся ak, равно 1, а основание межразрядной показательной функции не равно 1.
Дробные числа записываются в виде:
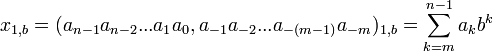, где:
m - число цифр дробной части числа x1,b.