Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Система остаточных классов (СОК)
Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей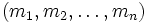 
с произведением 
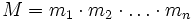так, что каждому целому числу x из отрезка [0,M 1] ставится в соответствие набор вычетов
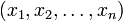, где
…
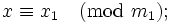
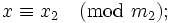
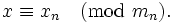
При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка [0,M 1].
В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в [0,M 1].
Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям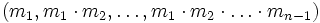 
.
Перевод чисел из СОК в десятичную систему счисления
Формула перевода имеет вид:
P = p1* p2* …* pn;
r = 0,1,2,… (целые числа), причём r выбирают так, чтобы разность между левой и правой частью выражения была меньше P;
Пример:
P = p1*p2*p3 = 3*5*7 = 105.
B1 = 105/3*k1 = 35*2 =70;
B2 = 105/5*k2 = 21*1 =21;
B3 = 105/7*k3 = 15*1 =15;
A = 2*70+4*21+6*15 — r*105;
A = 314 — r*105 = 104, где r=2.
Смешанная система счисления
Смешанная система счисления является обобщением b-ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел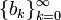 
и каждое число xпредставляется как линейная комбинация:
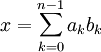, где на коэффициенты ak (называемые как и прежде цифрами) накладываются некоторые ограничения.
Записью числа x в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса k, начиная с первого ненулевого.
В зависимости от вида bk как функции от k смешанные системы счисления могут быть степенными, показательными и т. п. Когда bk = bk для некоторого b, показательная смешанная система счисления совпадает с b-ричной системой счисления.
Наиболее известным примером смешанной системы счисления являются представление времени в виде количества суток, часов, минут и секунд. При этом величина d дней h часов m минут s секунд соответствует значению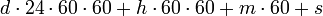 
секунд.
Факториальная система счисления
В факториальной системе счисления основаниями являются последовательность факториаловbk = k, и каждое натуральное число x предствляется в ви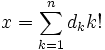де:
где:
