
Поиск
Десятичная система счисления
Десятичная система счисления — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем счисления в мире. Для записи чисел наиболее часто используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.
Десятичная непозиционная система счисления с единичным кодированием десятичных цифр возникла во второй половине третьего тысячелетия до н.э. в древнем Египте. В другой великой цивилизации - вавилонской - за две тысячи лет до н.э. внутри шестидесятеричных разрядов использовалась позиционная десятичная система счисления с единичным кодированием десятичных цифр.
Позиционная десятичная система счисления используется евреями с XIV в. до н.э. по сей день. Древнейшая известная запись позиционной десятичной системы обнаружена в Индии в 595 г. Нуль в то время применялся не только в Индии, но и в Китае. В этих старинных системах для записи одинакового числа использовались символы, рядом с которыми дополнительно помечали, в каком разряде они стоят. Потом перестали помечать разряды, но число всё равно можно прочитать, так как у каждого разряда есть своя позиция. А если позиция пустая, её нужно пометить нулём. В поздних вавилонских текстах такой знак стал появляться, но в конце числа его не ставили. Лишь в Индии нуль окончательно занял своё место, эта запись распространилась затем по всему миру.
Индийская нумерация пришла сначала в арабские страны, затем и в Западную Европу. О ней рассказал среднеазиатский математик аль-Хорезми. Простые и удобные правила сложения и вычитания чисел, записанных в позиционной системе, сделали её особенно популярной. А поскольку труд аль-Хорезми был написан на арабском, то за индийской нумерацией в Европе закрепилось неправильное название — «арабская».
Один десятичный разряд в десятичной системе счисления иногда называют декадой.
В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.
Десятичная система счисления является сдвоенной показательной позиционной десятичной системой счисления в которой основания основной системы счисления и вспомогательной системы счисления совпадают и равны 10. Дробные числа записываются в виде строки цифр с разделителем (десятичная запятая) и индексом:
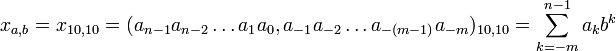
где: n - число разрядов целой части числа,
m - число разрядов дробной части числа, от 0 до бесконечности, при m=0 число целое,
k - число от -m до n-1, номер разряда,
a=10 - число, основание внутриразрядной системы счисления,
ak - числа в разрядах из замкнутого множества a={0,1,2,3,4,5,6,7,8,9}, цифры представляемого числа, x10,10,
b=10 - число, основание межразрядной системы счисления,
10k - числа межразрядной десятичной показательной функции, весовые коэффициенты bk разрядов.
Внутриразрядный индекс - a часто опускается, нередко опускается и межразрядный индекс - b.
Из комбинаторики известно, что число записываемых кодов не зависит от основания показательной функции - b, которое определяет диапазон представляемых числами x10,b величин, и равно числу размещений с повторениями:
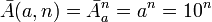
где: a=10 - 10-ти элементное множество a={0,1,2,3,4,5,6,7,8,9} из которого берутся цифры ak, n - число элементов (цифр) в числе x10,b.
Десятичная система счисления является комбинацией (произведением) двух зависимостей (функций). Внутри каждого разряда зависимость (функция) линейная f(ak)=ak, ak из множества a={0, 1, 2, 3, ..., 9}, между разрядами же зависимость нелинейная показательная - f(b,k)=bk=10k, bk из множества bk={1, 10, 100, ...}.
Цифры внутри разрядов ak могут быть записаны в разных кодах. Например, при их записи в двоичном коде получается двоично-десятичное кодирование, описанное ниже. При их записи в троичном коде, получается троично-десятичное кодирование. При их записи в десятичном коде, получается десятично-десятичное кодирование. Система счисления при этом не изменяется и остаётся прежней.
В двоичных компьютерах применяют двоично-десятичное кодирование десятичных цифр (Binary-Coded Decimal), при этом для одной двоично-десятичной цифры отводится четыре двоичных разряда (двоичная тетрада). Так как четыре двоичных разряда имеют 16 состояний, то при двоично-десятичном кодировании 6 из 16 состояний двоичной тетрады не используются.
Тавлица сложения в десятичной системе счисления
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 10 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Тавлица умножения в десятичной системе счисления
| * | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |


