Фибоначчиева система счисления
Любому неотрицательному целому числу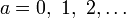 
можно единственным образом представить через последовательность битов: 
, причём последовательность {?k} содержит лишь конечное число единиц, и не имеет пар соседних единиц:
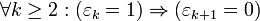. За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
Обоснование
В основе лежит теорема Цеккендорфа — любое неотрицательное целое число представимо в виде суммы некоторого набора чисел Фибоначчи, не содержащего пары соседних чисел Фибоначчи. Причём представление такое единственно.
Доказательство существования легко провести по индукции. Любое целое число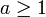 
попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого 
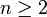верно неравенство: 
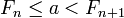. Таким образом, a = Fn + a', где
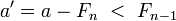, так что разложение числа a' уже не будет содержать слагаемого
Fn * 1.
Использование в теории информации
На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системы счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1.
Арифметика
При сложении чисел в позиционных системах счисления приходится выполнять перенос, то есть устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 0 = 10. В фибоначчиевой системе дело обстоит намного сложнее. Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только вправо, но и влево: 0200 = 1001. При переносе в отсутствующие разряды
Обобщение на действительные числа
Похожее устройство имеет позиционная система счисления для действительных чисел, основанием которой служит золотое сечение
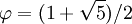— иррациональное число. Оказывается, что любое действительное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения:
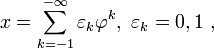
где {?k} обладает тем же свойством отсутствия соседних единиц. Коэффициенты находятся последовательным сравнением x с
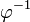— золотым сечением отрезка [0,1], вычитанием
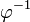(если ?k=1) и умножением на 
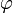Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение:
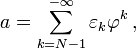
где N таково, что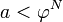 
. Разумеется, следует считать что
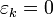для всех 
.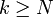