
Поиск
Удивительные свойства системы счисления Бергмана
Математическое выражение для системы счисления Бергмана имеет следующий вид:
где A - некоторое действительное число и ai - двоичные цифры, 0 или 1, i = 0, ±1, ±2, ±3, ti -
вес i-й цифры в системе счисления, t - основание системы счисления.
На первый взгляд, не существует никакой особенности в выражении по сравнению с известными позиционными системами счисления, но это только на первый взгляд. Главная особенность состоит в том, что Бергман использовал иррациональное число 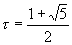 ("золотая пропорция") в качестве основания своей системы счисления, названной им "тау-системой".
("золотая пропорция") в качестве основания своей системы счисления, названной им "тау-системой".
Рассмотрим "тау-систему" с вычислительной точки зрения. Ее основание t определяет все необычные свойства системы счисления. Мы знаем из предыдущих страниц Музея, что "золотая пропорция" обладает следующим свойством: tn = tn-1 + tn-2.
Рассмотрим представления чисел в "тау-системе". Ясно, что сокращенная запись числа A в "тау-системе" имеет следующий вид:
A = anan-1 ... a1a0, a-1a-2 ... a-m.
Мы можем видеть, что сокращенная запись числа A представляет собой двоичную кодовую комбинацию, разделенную запятой на две части, левую часть
anan-1 ... a1a0,
соответствующую "весам":
tn, tn-1, ..., t1, t0 = 1,
и правую часть
a-1a-2 ... a-m,
соответствующую "весам": t -1, t -2, ..., t -m.
Заметим, что "веса" ti (i =0, ±1, ±2, ±3, ...) задаются математической формулой.
Например, рассмотрим двоичную кодовую комбинацию 100101. Ясно, что она представляет собой следующее действительное число:
A = 100101 = t5 + t2 + t0.
Используя формулу Бине, мы можем поучить, что число A, задаваемое выражением, равно:
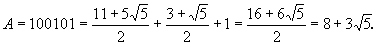
Заметим, что число 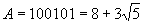 является иррациональным числом. Это означает, что мы представили некоторое иррациональное число A в "тау-систем", используя кодовую комбинацию 100101, состоящую из конечного числа бит!
является иррациональным числом. Это означает, что мы представили некоторое иррациональное число A в "тау-систем", используя кодовую комбинацию 100101, состоящую из конечного числа бит!
Ясно, что основание "тау-системы" представляется в ней традиционным образом, то есть:
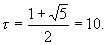
Но из нашего предыдущего опыта мы знаем, что невозможно представить иррациональное число с использованием конечного числа цифр. Именно поэтому возможность представления некоторых иррациональных чисел (степеней "золотой пропорции" и их сумм) с использованием конечной совокупности двоичных цифр есть первый неожиданный результат "тау-системы", который противоречит нашим традиционным представлениям о системах счисления.
Возникает вопрос о представлении натуральных чисел в "тау-системе". Для этого рассмотрим еще раз фундаментальное тождество. На кодовом уровне оно имеет следующую кодовую интерпретацию:100 = 011.
Как мы можем использовать кодовое преобразование Для этого мы рассмотрим "золотую" кодовую комбинацию 100101, которая представляет число. Если мы используем преобразование к старшим трем разрядам "золотой" кодовой комбинации" 100101, мы получим новое "золотое" представление числа, а именно:
A = t5 + t2 + t0 = 100101 = 011101 = t4 + t3 + t2 + t0.
Заметим, что в этом случае степень "золотой пропорции" t5 заменятся на сумму двух предыдущих степеней t4 + t3 в соответствии с фундаментальным соотношением. Заметим также, что это не изменяет число. На кодовом уровне такое преобразование представляет собой следующее: 100 ® 011.
Это кодовое преобразование называется "разверткой". Обратное преобразование 011 ® 100.
называется "сверткой".
Таким образом, числа имеют многозначное представление в "тау-системе". Это - второй неожиданный результат, вытекающий из рассмотрения "тау-системы". Используя введенные выше преобразования "свертки" и "развертки", мы можем получить два крайних "золотых" представления одного и того же числа в "тау-системе". Например, рассмотрим кодовую комбинацию 0111111. Если мы выполним в ней все возможные "свертки" (7), то мы получим первое крайнее "золотое" представление, называемое "минимальной формой":
0111111 = 1001111 = 1010011 = 1010100
("минимальная форма").
Заметим, что в "минимальной форме" двух единиц рядом не встречается.
Рассмотрим теперь "золотую" кодовую комбинацию 100000, которая представляет иррациональное число 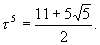 Выполняя в ней все возможные операции "развертки", мы можем получить второе крайнее "золотое" представление, называемое "максимальной формой":
Выполняя в ней все возможные операции "развертки", мы можем получить второе крайнее "золотое" представление, называемое "максимальной формой":
100000 = 0110000 = 0101100 = 0101011
("максимальная форма").
Заметим, что в "максимальной форме" двух нулей рядом не встречается.
Покажем теперь, как можно получить все "золотые" представления натуральных чисел, используя операции "свертки" и "развертки". Начнем с числа 1. Оно может быть представлено через "золотую пропорцию" следующим способом:
1 = t0.
Но используя "тау-систему", мы можем представить число
t0 = 1
следующим образом:
1 = t0 = 1,00.
Заметим, что в "золотом" представлении 1,00 запятая отделяет 0-й разряд от разрядов с отрицательными индексами.
Затем, используя "развертку", мы можем представить число следующим образом:
t0 = 1,00 = 0,11 = t -1 + t -2.
А теперь добавим бит 1 в 0-й разряд "золотого" представления 0,11. В результате мы получим "золотое" представление числа 2: 2 = 1,11.
Применяя операцию "свертки" к старшим разрядам "золотого" представления, мы получаем новое "золотое" представление ("минимальную форму") числа 2:
2 = 10,01 = 1 + t -2.
Добавляя бит 1 в 0-1 разряд "золотого" представления числа 2, мы получаем "золотое" представление" числа 3:
3 = 11,01.
Применяя операцию "свертки" к старшим разрядам "золотого" представления числа 3, мы получаем новое "золотое" представление ("минимальную форму") числа 3:
2 = 100,01 = t2 + t -2.
"Золотые" представления чисел 4 и 5 имеют следующий вид:
4 = 101,01 = t2 + t0 + t -2;
5 = 1000,1001 = t3 + t -1 + t -4.
5 = 1000,1001 = t3 + t -1 + t -4.
Продолжая этот процесс, можно получить "золотые" представления всех натуральных чисел в "тау-системе". Это означает, что любое натуральное число может быть всегда представлено в виде конечной суммы степеней золотой пропорции! Это утверждение представляет собой наиболее неожиданный результат, вытекающий из рассмотрения "тау-системы".
А теперь возвратимся на 2,5 тысячелетия назад и представим себе реакцию пифагорейцев на это утверждение. Согласно главной доктрине пифагорейцев "Все есть число" в основе мироздания лежат натуральные числа и их отношения, так как любую вещь в природе можно выразить как отношение двух натуральных чисел. Но мы только что показали, что любое натуральное число может быть выражено через золотую пропорцию. Из этого рассуждения с необходимостью вытекает новая доктрина, которую пифагорейцы немедленно сформулировали бы, если бы знали о нашем результате: "Все есть золотая пропорция"!
Но пифагорейцы были бы потрясены еще больше, если бы знали, что натуральные числа обладают еще одним уникальным свойством - Z-свойством, о котором мы расскажем на следующей страничке нашего сайта. Следуйте за нами!


